半分に折ったり対角線を測ったり…コピー用紙にひそむ不思議な数学!
今日は2022年2月22日。ずらりと「2」が並んでいます。
数学において2の話題というと、2が唯一の偶数の素数であることや、2次方程式や2次関数、1/2という分数などが思い浮かびます。今回は2の正の平方根、つまり、2乗すると2になる数「√2」の話をご紹介しましょう。
「無理数」の発見
√2という数は、意外にも私たちがふだん使っているコピー用紙やノートなどの長方形にひそんでいます。√2は、1辺の長さが1の正方形の中に存在していて、対角線の長さが√2になります。
√2を小数で表すと、
√2=1.41421356…
となります。そして、√2は分数、つまり整数の比ではありません。
古代ギリシャのピタゴラスの時代には、整数の比で表すことのできない数が存在するということが信じられませんでした。√2が整数の比で表すことのできない数であることに驚いたピタゴラスは、「これは神がこの世を創り間違えたのだ」といって、このことを発見した弟子を地中海に沈めてしまったというような言い伝えが残っているほどです。
√2の発見は、整数の比で表すことのできない数、すなわち「無理数」の発見だったのです。
コピー用紙を半分に折ると……?
√2は、私たちの身のまわりに存在しています。ふだん使っているコピー用紙やノートなどの長方形の縦と横の長さの比がどのようになっているか、考えたことがあるでしょうか。
コピー用紙を半分に折ると、元の長方形と同じ形の長方形になります。つまり、縦と横の長さの比が同じ「相似な長方形」になります。これがとても機能的であることはいうまでもありません。
用紙の縦と横は使い方によるので、以下、短辺、長辺とよぶことにします。じつは、この長方形の用紙の短辺と長辺の長さの比が1:√2になっているのです。長方形の用紙を半分に折ったとき、同じ形の長方形になるためには、短辺と長辺の長さの比が1:√2になっていなければなりません。
その理由は?
理由は以下のとおりです。このような性質をもった長方形の短辺と長辺の長さの比を1:xとすると、半分に折ってできた長方形の短辺と長辺の長さの比は、x/2:1になります。
もとの長方形と半分に折った長方形の短辺と長辺の長さの比は同じなので、
1:x=x/2:1
となります。内項の積と外項の積は等しいので、
x²/2=1
となります。これより、
x²=2
という2次方程式ができ、これを満たすxの値は√2であることがわかります。つまり、紙を半分に折って同じ形の紙ができるためには、短辺と長辺の長さの比が1:√2でなければならないことがわかります。
このように、毎日使っている用紙やノートに√2という数がひそんでいるのです。
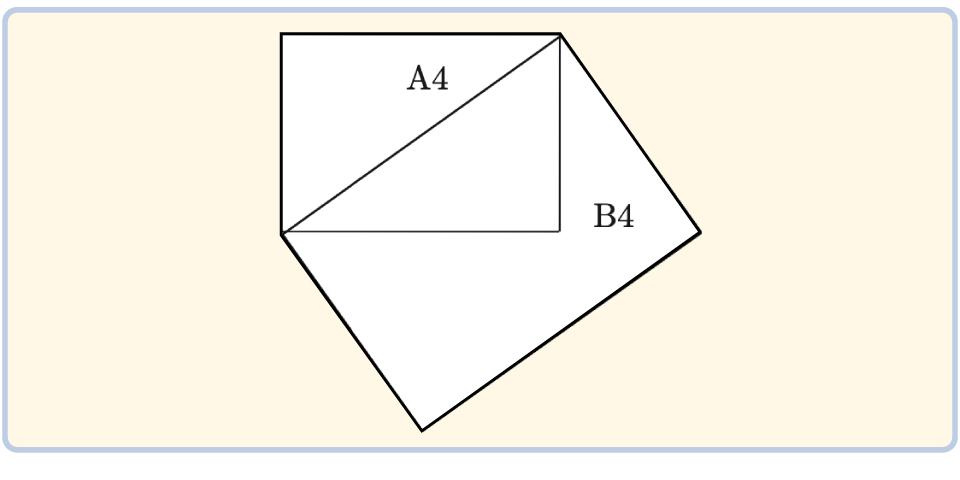
ところで、私たちが日常的に使用しているコピー用紙やノートのサイズには、「A判」と「B判」があります。B4判の長方形の長辺をA4判の長方形の対角線に合わせると、ピタッと一致することをご存じでしょうか?
 notebook-laptop
notebook-laptop