Folding in half or measuring diagonal lines ... Mysterious mathematics that hits a copy paper!

Today is February 22, 2022."2" is lined up.

In mathematics, the topic of 2 is that 2 is the only prime of the even number, a secondary equation, a secondary function, and a fraction of 1/22.This time, let me introduce the positive square root of 2, that is, the number of "√2" that is 2 when you ride 2.

Discovering "impossible numbers"

The number √2 is surprisingly hidden in rectangles such as copy paper and notebooks we usually use.√2 exists in a square with one side length, and the diagonal length is √2.

When √2 is expressed as a small number,

√2 = 1.41421356 ...

Will be.And √2 is not a fraction, that is, an integer.

I can't believe that in the ancient Greek Pythagoras era, there were an inseparable number of integers.Pythagoras was surprised that √2 was an inseparable number of integer ratio, and said, "This is a mistake that God created this world."There is a legend that remains.

The discovery of √2 was a number that could not be represented by the integer, that is, the discovery of "no reason".

If you fold the copy paper in half ...?

√2 is around us.Have you ever wondered how the vertical and horizontal lengths of rectangles, such as copy paper and notebooks you usually use are?

If you fold the copy paper in half, it will be a rectangle of the same shape as the original rectangle.In other words, the ratio of vertical and horizontal length is the same "similar rectangle".It goes without saying that this is very functional.

Since the vertical and horizontal of the paper depends on how it is used, the following is the short side, the long side.In fact, the ratio of the short side of this rectangular paper and the length of the long side is 1: √2.When a rectangular paper is folded in half, the ratio of the short side and the long side must be 1: √2 in order to become a rectangle of the same shape.

The reason is?

The reason is as follows.If the ratio of the short side of the rectangle and the length of the long side with such properties is 1: x, the ratio of the rectangular short side and the long side that is folded in half is x/2:It will be 1.

The ratio of the original rectangle and the length of the long side of the rectangle that folded into half are the same, so

1: x = x/2: 1

Will be.Since the accumulation of the internal section and the accumulation of the outer items are equal,

X²/2 = 1

Will be.Than this,

X² = 2

You can see that the value of the X that satisfies this is √2.In other words, in order to fold the paper in half and make paper of the same shape, the ratio of the short side and the long side must be 1: √2.

In this way, the number of √2 is hidden in the paper and notebooks used every day.

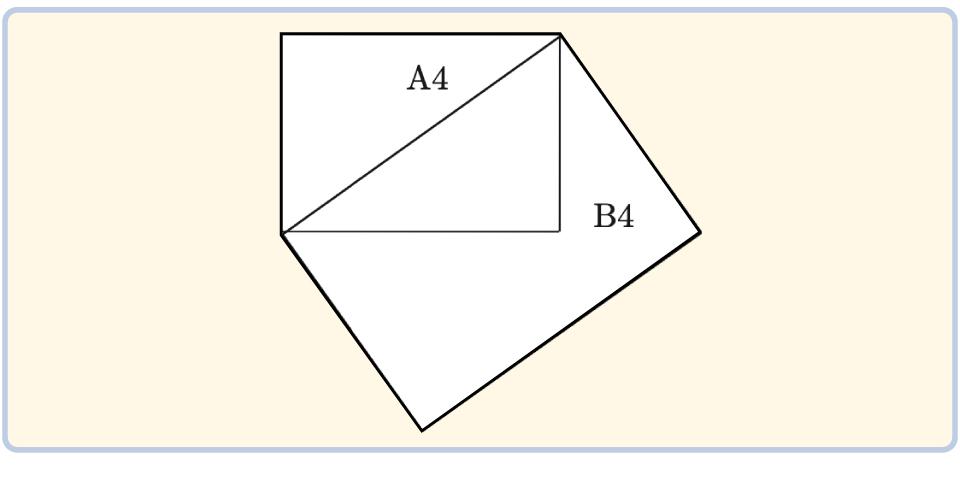
By the way, the size of copy paper and notebooks we use on a daily basis includes "A -form" and "B format".Did you know that if you match the long side of the rectangular rectangle to the diagonal of the A4 size rectangle, it matches perfectly?